This Model Teaches AI to Handle Long-Term Memory Like a Computer

Table of Links

Abstract & Introduction

Methods

Methods Part 2

Experimental Results

Experimental Results Part 2

Related Works, Discussion, & References

Appendix A, B, & C

Appendix D

3. Experimental Results

In §3.1-3.3, our chosen tasks are representative of various types of symbolic reasoning and wellknown benchmarks to measure the symbol-processing capability of ML models. To showcase that these tasks are non-trivial, we report how Chat-GPT failed on our tasks in Appendix D.6. We validate the contribution of our methods in other practical tasks in §3.4. We also explain the choice of competing baselines in Appendix D.

3.1 Algorithmic Reasoning

In our first experiment, we study the class of symbol processing problems where an output sequence is generated by a predefined algorithm applied to any input sequence (e.g., copy and sort). The tokens in the sequences are symbols from 0 to 9. The input tokens can be coupled with meta information related to the task such as the priority score in Priority Sort task. During training, the input sequences have length up to L tokens and can grow to L + 1, 2(L + 1), 4(L + 1) or 8(L + 1) during testing. Our setting is more challenging than previous generalization tests on algorithmic reasoning because of four reasons: (1) the task is 10-class classification, harder than binary prediction in Graves et al. [2014], Le and Venkatesh [2022], (2) the testing data can be eight time longer than the training and the training length is limited to L ≈ 10, which is harder than Grefenstette et al. [2015], (3) there is no curriculum learning as in Kurach et al. [2015], and (4) the training label is the one-hot value of the token, which can be confusing in case one token appears multiple times in the input sequence and tougher than using label as the index/location of the token as in Vinyals et al. [2015].

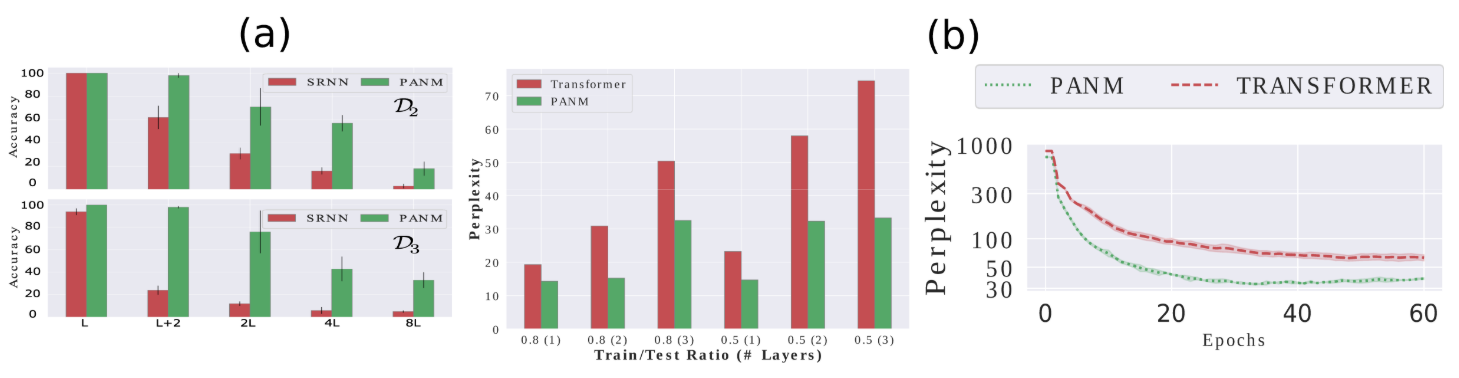
Baselines are categorized into 4 groups: (1) Traditional RNNs such as LSTM [Hochreiter and Schmidhuber, 1997], (2) Sequential attention models: Content Attention [Bahdanau et al., 2014], Location Attention [Luong et al., 2015], Hybrid Attention (our baseline concatenates the attention vectors from content and location attention), (3) MANNs such as NTM [Graves et al., 2014], DNC [Graves et al., 2016], Neural Stack [Grefenstette et al., 2015] and Transformer [Vaswani et al., 2017], and (4) pointer-aware models: NRAM [Kurach et al., 2015], PtrNet [Vinyals et al., 2015], ESBN [Webb et al., 2020] and our method PANM. In this synthetic experiment, we adopt LSTM as the encoder for PANM. All baselines are trained with fixed number of steps (100K for ID Sort and 50K for the rest), which is enough for the training loss to converge. For each task, each baseline is trained 5 times with different random seeds and we use the best checkpoint on L + 1 mode validation to evaluate the baselines.