Author:
(1) K. Razi Naqvi, Department of Physics, Norwegian University of Science and Technology (NTNU), 7094 Trondheim, Norway
Table of Links
3 Comments elicited by the solution to Milne’s problem for B-particles
6 Concluding remarks and References
6 Concluding remarks

The claim—motivated by the search for a better boundary condition—that the Lorentz model is a useful tool for investigating bimolecular reactions in solutions became credible only after the publication of Burschka and Titulaer’s numerical solution of the one-dimensional KKE [4]. Immediately prior to that, one critic expressed the “community opinion” by stating in a referee report (on an article co-authored by me) that the LBE “is absolutely useless in dealing with transport in liquids”, and insisted that this task is best handled by solving the KKE. Only then did the need arise for comparing the length scales of inverse and regular Brownian motion. The Trondheim group has shown that inverse Brownian motion, regular Brownian motion and the BGK-model are indistinguishable at the DE-level, provided that one uses the appropriate BC [31], namely that stated in Eq. (20). A Procrustean random walk model that allows no distribution of path lengths seems (to me) unphysical, much like the lattice model that informed Smoluchowksi’s thinking (about the boundary condition at an absorbing surface), and has misinformed generations of students as well as aficionados of chemical kinetics.
Infinitely heavy B-particles, infinitely light L-particles, infinitely inflexible (about the constancy of their pathlenghts) R-particles are all fictions, but some fictions are more fruitful than others, and some are outright useless. Whether the fiction of R-particles will bear fruit (in the setting of diffusion-mediated reactions) or serve as a mere distraction remains to be seen.
A Milne’s problem: calculating the density profiles
The purpose of this appendix is to enable a reader of this article to generate the data used for plotting the density profiles shown in Fig. 1.
The density data for L-particles were generated with the aid of a variational calculation [32], in which ℓ was used a the unit of length. The corresponding data for B-particles were computed by improving the results obtained by the Trondheim group through a half-range treatment [10], in which the 𝑁th order approximation for the particle density 𝑛 was expressed in the form
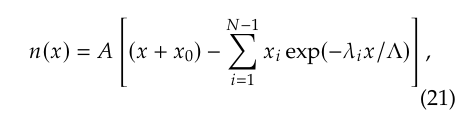
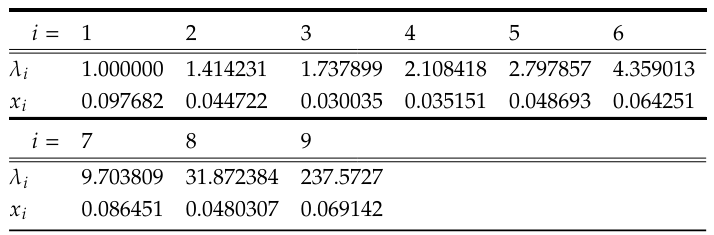
and values of 𝑥0 (1.459877Λ), 𝑥𝑖 and 𝜆𝑖 (for 𝑖 =1–8) resulting from a ninth-order approximation (𝑁 = 8) were reported, and the values of 𝑛(𝑥) close to the wall were compared with those found by Marshall and Watson (M&W) on the basis of their exact analytical treatment [33]. The improvements consists of three minor changes: the value of 𝑥0 has been replaced by 𝑥0 = 1.460354Λ (the first seven figures of the exact result), one more term has been added, and the values of 𝑥𝑖 and 𝜆𝑖 for the last three terms (𝑖 =7–9) have been optimised in a least-squares fit to the numbers in column (A) of Table 1 of M&W. The complete set of {𝑥𝑖 , 𝜆𝑖} values (of mostly-analytical-partly-empirical origin) is displayed in Table 1, the upper part of which is identical with Table II of ref. [10]. For plotting the density of B-particles in Fig. 1, the length scale was changed from Λ to ℓ.
References
[1] M. von Smoluchowski. Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen. Physik. Zeit., 17:568–571 (1st instalment), 585–593 (2nd instalment), 1916.
[2] M. von Smoluchowski. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. Phys. Chem. (Leipzig), 92:129–168, 1917.
[3] M. von Smoluchowski. Grundriß der Koagulationskinetik kolloider Lösungen. Kolloid Z., 21:98–104, 1917.
[4] M. A. Burschka and U. M. Titulaer. The kinetic boundary layer for the Fokker-Planck equation with absorbing boundary. J. Stat. Phys., 25:569–582, 1981.
[5] K. Razi Naqvi, K. J. Mork, and S. Waldenstrøm. Comment on “Steady, one-dimensional Brownian motion with an absorbing boundary”. J. Chem. Phys., 77(7):4263–4264, 1982.
[6] K. Razi Naqvi, K. J. Mork, and S. Waldenstrøm. Reduction of the Fokker-Planck equation with an absorbing or reflecting boundary to the diffusion equation and the radiation boundary condition. Phys. Rev. Lett., 49:304–307, 1982.
[7] K. Razi Naqvi, S. Waldenstrøm, and K. J. Mork. Kinetics of diffusion-mediated bimolecular reactions. A new theoretical framework. J. Phys. Chem., 86:4750–4756, 1982.
[8] K. Razi Naqvi, S. Waldenstrøm, and K. J. Mork. On the rate of absorption of Brownian particles by a black sphere: The connection between the Fokker–Planck equation and the diffusion equation. J. Chem. Phys., 78(5):2710–2712, 1983.
[9] Enrico Fermi (author) and Emilio Segre (chief editor). Collected Papers (Note E Memorie), (Vol. 1: Italy, 1921–1938). University of Chicago Press, Chicago, IL 1962.
[10] K. Razi Naqvi, K. J. Mork, and S. Waldenstrm. Steady-state, one-dimensional Fokker-Planck equation with an absorbing boundary: A half-range treatment. Phys. Rev. A, 40:3405–3407, 1989.
[11] S. Waldenstrøm, K. J. Mork, and K. Razi Naqvi. Milne problem for a hard-sphere Rayleigh gas: a study based on the Fokker-Planck equation. Phys. Rev. A, 28(3):1659–1661, 1983.
[12] S. V. G. Menon, Vinod Kumar, and D. C. Sahni. Green’s function approach to the solution of the time dependent Fokker-Planck equation with an absorbing boundary. Physica A: Statistical Mechanics and its Applications, 135(1):63–79, 1986.
[13] M. J. Lindenfeld and B. Shizgal. The Milne problem: A study of the mass dependence. Phys. Rev. A, 27:1657–1670, 1983.
[14] Knud Andersen and Kurt E. Shuler. On the relaxation of the hard-sphere Rayleigh and Lorentz Gas. J. Chem. Phys., 40(3):633–650, 1964.
[15] B. Davison. Neutron Transport Theory. OUP, Oxford, 1957.
[16] Julian Keilson and James E. Storer. On Brownian motion, Boltzmann’s equation and the Fokker-Planck equation. Quarterly of Applied Mathematics, 10(3):243–253, 1952.
[17] M. R. Hoare. The linear gas. In Ilya Prigogine and Stuart A. Rice, editors, Advance in Chemical Physics, volume 20, pages 135–214. Wiley-Interscience, New York, 1971.
[18] Marie Smoluchowski. Sur le chemin moyen parcouru par les molécules d’un gaz et sur son rapport avec la théorie de la diffusion. Bull. Acad. Sci. Cracovie, pages 202–213, 1906.
[19] K. Razi Naqvi. 100+ years of colossal confusion on colloidal coagulation. Part I: Smoluchowski’s work on absorbing boundaries. arXiv:2404.17021 [cond-mat.stat-mech], pages 1–20, 2024.
[20] Robert M. Ziff. Flux to a trap. J. Stat. Phys., 65(5):1217–1233, 1991.
[21] S. N. Majumdar, A. Comtet, and R. M. Ziff. Unified solution of the expected maximum of a discrete time random walk and the discrete flux to a spherical trap. J. Stat. Phys., 122(5):833– 856, 2006.
[22] R. M. Ziff, S. N. Majumdar, and A. Comtet. General flux to a trap in one and three dimensions. J. Phys.: Condens. Matter, 19(6):065102, 2007.
[23] H. L. Frisch and F. C. Collins Diffusional processes in the growth of aerosol particles. J. Chem. Phys., 20:1797–1803, 1952.
[24] F. C. Collins and G. E. Kimball. Diffusion-controlled reactions in liquid solutions. Ind. Eng. Chem., 41(11):2551–2553, 1949.
[25] D. C. Sahni. The effect of a black sphere on the flux distribution in an infinite moderator. J. Nucl. Energy, 20(11):915–920, 1966.
[26] M.M.R. Williams. A simple method for calculating the linear extrapolation distance at the surface of a black body. Annals of Nuclear Energy, 15(2):101–105, 1988.
[27] Vinod Kumar and S. V. G Menon. Condensation rate on a black sphere via Fokker-Planck equation. J. Chem. Phys., 82(2):917–920, 1985.
[28] M. E. Widder and U. M. Titulaer. The kinetic boundary layer around an absorbing sphere and the growth of small droplets. J. Stat. Phys., 55(5/6):1109–1127, 1989.
[29] S. Waldenstrøm and K. Razi Naqvi. The steady rate of absorption (by a grey sphere) of particles obeying the Fokker-Planck equation: analysis of the results obtained by moment methods. Ark. Fys. Seminar Trondheim, (4):1–37, 1988.
[30] Joel H. Hildebrand. Motions of molecules in liquids: Viscosity and diffusivity. Science, 174(4008):490–493, 1971.
[31] K. Razi Naqvi, K. J. Mork, and S. Waldenstrøm. Transport equations and boundary conditions for describing motion in a homogeneous solvent with a completely absorbing boundary. Ark. Fys. Seminar Trondheim, (7):1–36, 1982.
[32] K. Razi Naqvi. Milne’s problem for a non-capturing medium: accurate analytic approximations for particle density and emergent angular distribution. J. Quant. Spectrosc. Radiat. Transfer, 50(1):59–64, 1993.
[33] T. W. Marshall and E. J. Watson. The analytic solutions of some boundary layer problems in the theory of Brownian motion. J. Phys. A: Math. Gen., 20(6):1345–1354, 1987.
This paper is available on arxiv under CC BY 4.0 DEED license.

